The Gamble
Pierre Raymond de Montmort in his treatise of gambling chances “Essay d'analyse sur les jeux de hazard” described the following game of chance (paraphrasing liberties taken):
“A deck of N cards is labeled 1....N and shuffled. The player starts counting from 1 as the dealer flips this shuffled deck of cards over one by one in turn. If the player sees a card with the same value as she counts (i.e on the 2nd flip the card is card number 2) the player wins. Otherwise the player loses.”
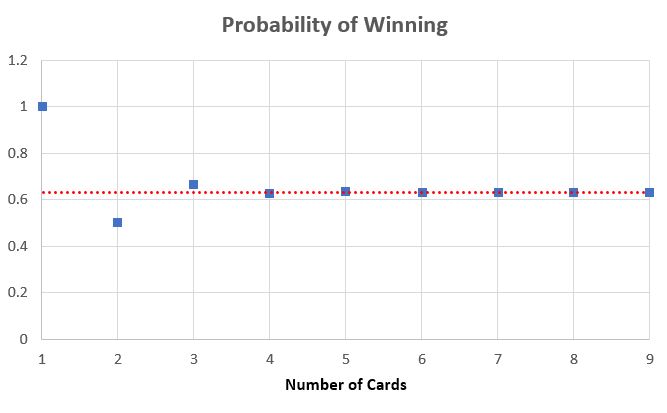
I have built a simulation of the game for 10 cards on my coding page. What is the chance of winning this game? The key to answering this is the inclusion-exclusion principle.
A Solution
As with all mathematical probability questions, a difficult starting point is naming the sample space and included relevent events. The sample space here must be thought of broadly as the set of all possible arrangments of the deck, of which there are N!=N(N−1)(N−2)…(2)(1). Considering just each flip runs into issues with independence when trying to extrapolate to the entire run of cards. Consider the event Ej= card j matches, so the chance to win (getting at least one match) would be P(E1∪E2∪⋯∪EN)
A way to relate a union of a bunch of sets to their intersections is to add all sets, subtract off the 2-pair intersections, add in the 3-pair intersections as it was subtracted off mistakenly, subtract the 4-pair intersections, etc. We then need to examine the intersection events themselves starting with just one event:
P(Ej)
Imagine not showing any cards and wanting to pick, out of the N cards, your current number. Assuming each is equally likely (intrinsic to Prof. Blitzstein’s so-called naive definition of probability) this reduces to the chance of picking one exact card from N leading to:
P(E_j) = \frac
Consider now the 2-pair: E1∩E2. This amounts to counting how many ways to arrange the rest of the deck if the first two match, therefore:
P(E_1 \cap E_2) = \frac
Extend this to the k-pair: E1∩E2∩⋯∩Ek. Notice if k=N then it is 1/N! as we are asking for a complete match, only 1 possible shuffling out of the total.
P(E_1 \cap \dots \cap E_k) = \frac
Start with adding all single events (one match) then subtracting the double events (2 matches) due to overcounting, etc to get:
P(E1∪E2∪⋯∪EN)= = \binom \frac - \binom \frac + \binom \frac - \dots + (-1)^ \binom \frac
= 1 - \frac + \frac - \frac + \dots + \frac \approx 1-e^
Notice that the finite sum comes out exactly to an N-term Taylor series approximation to 1-e^ ! The convergence is uniform as ez is a quintessential entire function, with incredibly fast convergence speed as the error term of approximation is O(1/N!) (seen below).
Orange = 1-exp(-1) with the blue being truncated Taylor series approximations
A Solution to Particular Cases
What about the chance that you have exactly m matches in a game? It is hard to think of the amount of arrangments which have strict requirements like exactly m matches (at least for difficult values of m), though appealing to another probability trick (and general life strategy) we can avoid this responsibility by doing the complete opposite. The number of arrangments with no matches (a derrangement denoted D) given N cards would be (total number of arrangments possible) - (all 1-match arrangments + all 2-match + … + all N match arrangments):
D= N! - \sum_^N (-1)^ \binom (N-j)!
= N! - N!\sum_^N \frac
= N! \left( 1 + \sum_^N \frac \right)
D= N! \sum_^N \frac
To grab an arrangment that has say m matches just pick the numbers that match. Of N cards we are choosing m without replacement and order does not matter so \binom arrangments fulfill this. However we now need to pick the rest of the cards to NOT match! How many derrangments can be made from N−m cards? The above says N! \sum_ \frac, putting this together:
\text{Num of Arrangments with }m \text = \binomN! \sum_ \frac
The probability of m matches now is just to divide this value by the total number of arrangments N! to get:
P(m \text ) = \binom \sum_ \frac
For N = 10, the probability of getting 9 matches is zero but 10 matches is not! Why do you think that is?
Philosophical Implications
If one considers the deck of cards getting huge N→∞ then a typical conjecture is that the chance to win is 100% since of course sooner or later the number would match due to some infinite monkey thought experiment justification. Another usual suspicion is that the chance to win would vanish to 0% since the deck is just so massive, how could one possibly hope on getting one exact matching number on any one flip? There is a fundamental struggle between each match becoming more unlikely (more cards so less chance) and the fact that you get more cards to try to match (more cards so more chance). In the face of these human intuitions mathematics then comes in and says the answer is 1-e^, a seemingly preposterous value synonomous with continuous processes, in a discrete counting situation no less. I was able to prove with Taylor theory that not only were those intuitions incorrect, those intuitions diverge at uniform speeds which is a level of wrongness nearly nonexistent in the real world.
When tragedy befalls people, thoughts that usually come up are “Why me?” or “Why not someone else“. When someone wins the lottery there seems to be a lot less questions and more statements about luck or rehashing of the “You can’t win if you don’t play” sentiment. Rigorous decision making or emotion setting with only qualitative estimates of probabilities seems impossible as humans share some supernatural or superstitious relationship with some undefined concept called “chance”.
“In war, which is an intense form of life, Chance casts aside all veils and disguises and presents herself nakedly from moment to moment as the direct arbiter over all persons and events”
It it certainly easy to poke at the psychology of probability and how flawed it is but assuming a perfect understanding of the mathematical argument, does that potentially construct some bridge between a more grounded intuition and circumspect in other problems? The answer evidently is no, as a perfect understanding of this argument and its techniques makes similar questions of chance easier to tackle but not easier to intuit. There is no objective connection to be made between the numerical answer and the problem statement at large, not even in retrospect. The counting aspect of this problem I think is the main culprit, even as problems remain finite it is possible to convolute problems to make the counting extremely difficult (though not theoretically impossible given that cases are clearly defined). Naturally if we assume there is an omni-counter (someone who can perfectly count all finite cases of any finite chance problem), would this omni-counter have transferrable intuition about the apparent limiting clash between number of cards creates more chances to be right (more cards = more chance) and that the chance to be right about any one card diminishes (more cards = less chance)?