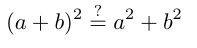In every level of mathematics, particularly in elementary and high schools, teachers use heuristics to get concepts across to students. Even before the dot com boom, we knew that all learning is distance learning, with only proximity to the students changing while the fact remains that concepts need to travel from a teachers’ brain to a students’. It is entirely the case that concepts are whittled of subtleties or interesting extremal examples in favor of raising test scores through substituting critical thinking with pure “mechanics“. In this new tagged series Bad Heuristics inspired by this MathOverflow question I philosophize on some of these teaching practices.
What is meant by a “bad” heuristic?
A tentative first definition of bad heuristic is drawn up in regards to two main offenders; under-emphasis of mathematical detail and over-emphasis of mechanical writing:
“A method of explanation or methodology itself which forgoes details of a mathematical concept knowingly or otherwise in favor of mechanical solutions. ”
First what is meant by “mechanical solutions” is an instruction method with often a literal instruction of what to do with ones pencil when working on mathematical problems built in. As if the teacher is, perhaps out of pressure to teach to a certain class of questions, trying to force the hand of the test taker manually. Here are some heuristics guilty of this and each of which I hope to unpack in more detail in future posts:
First-Outside-Inside-Last (FOIL) methodology for binomial term multiplication.
A continuous function is one in which when you draw it, you “don’t pick up your pencil”.
Function evaluation is the same thing as “plug n’ chug” in a given formula.
The quadratic formula is memorized through song and not properly motivated or explained, simply the mechanics of writing it on paper are committed to memory.
The motif of these is that mathematics is reduced to algebraic manipulation. If a course exam is legislated to a small enough set of question types, a bad heuristic is one invariably drawn up to cut conceptual corners and have students instead memorize pencil movements or disconnected facts, not unlike teaching how to perform a piano song by skipping music theory in favor of explaining what buttons to press and when.
Why this definition does not include “incomplete” heuristics
Intuitively it seems a heuristic focusing purely on memorization of hand movements or sounds is “worse” than heuristics that do point to conceptual understanding though with some lacking details or failings in some extremal examples. I then elect to call such cases “incomplete” heuristics and so a “bad” heuristic can be thought of as an extension of these:
Multiplication is just repeated addition (also exponentiation is just repeated multiplication).
We “cannot” take the square root of a negative number.
Integration of a polynomial is a “reverse power rule” where you add one to the power and divide by the new power.
Each of these are just trying to facilitate an understanding of a concept though on a level below perhaps what will be required later in a students career or overlook a particular case (as in the case of natural logarithm in the last case). In any case, expounding on the concept or delving into cases can get students up to speed whereas in a “bad” heuristic conceptual understanding is purposefully replaced by structural routine.