The interpretation, objectiveness, and subjectiveness of "probability" or "chance" is a vast and especially new field to this author. Using the Whitepages of philosophers, PhilPeople, over 888 modern researchers confess their interest in the "Philosophy of Probability" with some focus on the three characteristics above. My goal from here, to benefit my own elucidation, is to briefly summarize and expound upon traditional schools of thought for the philosophy of probability seen in The Stanford Encyclopedia of Philosophy and other sources to be listed. Ultimately, this post is successful if the reader learns along with me.
My own purely mathematical training has a probability calculating structure involving "measures" happening on certain event spaces thought of as "sets" created in Kolmogorov's pivotal work [2]. However this abstract structure is left dusty if not briefly explained even for baccalaureate holders in mathematics and certainly is unapproachable for those otherwise. Notwithstanding, the news reports a certain chance of rain (i.e 70% chance of rain today) and people nod in agreement at the idea. What is this idea? Can some rigorous argumentation perhaps clarify such a statement for ordinary people? As far as science goes, this system provides adequate explanation and usefulness however philosophy will attempt to answer what exactly probabilities are.
The Philosophical Problem Statement
Can an all-knowing being predict all stochastic outcomes?
Are “probabilities” agent-independent? That is, do they exist in reality or are they only human based facts of ignorance. [6]
If probabilities exist in reality, what exactly do they represent?
Kolmogorov's Probability Calculus
“if this calculus be condemned, then the whole of the sciences must also be condemned.”
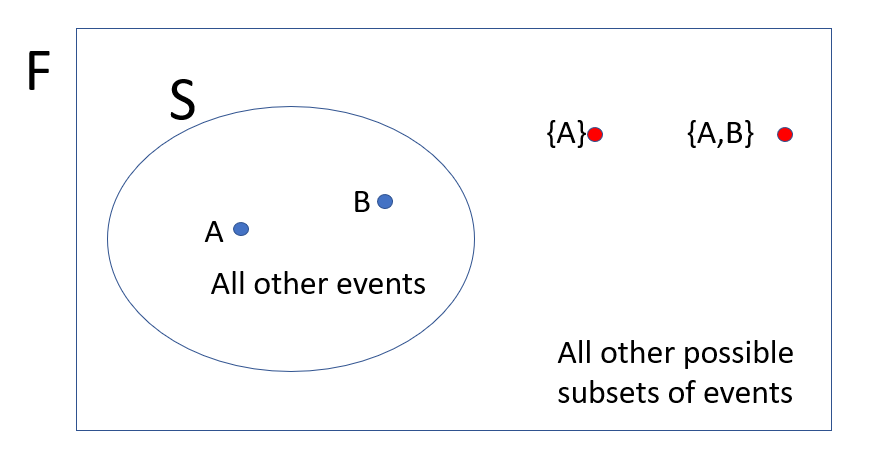
Andrey Kolmogorov pioneered a body of thinking which allowed for quantification/calculation with probability [1], this is the aforementioned sets and measures construction. We think of events (outcomes of a stochastic scenario) as individual elements contained in a big set S. As events may happen concurrently, we make a big bin containing possible subsets of S. The technical name for this bin is a field (also called an algebra), notated F, is constructed with the following axioms:
If A is a set of event(s) in F, then the complement of A is also in F; that is, A not happening is sensible.
If A,B are sets of event(s) in F, then their union is also in F; that is, concurrent events happening is sensible.
This structural logic is then F is a field containing all possibilities (subsets of S) such that combinations of the events (union, intersection, and complementation) are themselves possible events in the space. Furthermore, a function P called the "probability measure" exists so that we can assign a numerical chance (from 0 to 1) to the events of F. There are some natural restrictions on P:
P(A) must be non-negative; that is, something having a negative probability is nonsense.
P(S) = 1; that is, the probability of at least something from the set of all possibilities happening is 1 (100% chance).
P(A union B) = P(A) + P(B) for any events A,B in F such that A and B are disjoint; that is, the chance of two unrelated events occurring can be added from their individual chances of occurring.
The hierarchy of this structure is drawn below:
A,B are events contained in S (the sample space of all events) which is sitting in the field F containing all of S as well as the possible combinations of events in S.
It is important to note the order of definition. First F is defined , then allowing P to be defined; that is, F need not be the set of all subsets. For instance if we are tossing die, we could be interested in the event in an odd numbered face. The definition of F then could include odd or even results and miss specific results like 2 or 5 but still satisfy the axioms above. Interestingly, as noted in [2], this is not the only viable option for so called coherent axiom structure and so the question of "best" axiomization becomes entirely philosophical.
Unfortunately F also need not be finite; consider picking any decimal number between 0 and 1, here we have infinitely many possibilities. In such a case, a fourth axiom (countable additivity) becomes necessary:
P(infinite union of events) = Sum of all individual event probabilities
[6] mentions this is the most controversial axiom, drawing several interesting paradoxical thought experiments. The point philosophically is that this axiom asserts that individual events in an infinite list have probability 0, leading immediately to counterintuitive results.
An Explicit Example
The triple (S,F,P) forms a probability space altogether. Consider the experiment of flipping a fair coin twice, recording the result each time. Then the above structure can be written explicitly:
The possible events are contained in S = {H,T} where T = tails and H = heads.
The field containing the events and their set combinations is F = {S, {H} ,{S}, {}} where {} is the empty set.
Then P(S) = 1 (the chance of flipping heads or tails is 100%), P(H) = 50% = P(T) and P({}) = 0 as it must land on either heads or tails.
It is possible to explicitly write down these constructions in such a simple example and other slightly more complicated examples, but it quickly gets out of hand in more practical scenarios.
A Less Explicit Example
Consider Benford’s Law. In short, it is a counter-intuitive result that the leading significant digits of some real-world data-sets are not uniformly random. In fact they follow a skew-right distribution favoring low digits like 1,2,3 well over higher digits like 8,9. This result then becomes a viable tool for detecting fraud , as people who are faking numbers will create data that is “too uniformly random”. This effect can also be seen with students taking multiple choice exams, students often prefer changing an answer if the ones before it are the same answer.
The machinery of Kolmogorov can be implemented here as well. Consider the sample space as possible leading digits:
S = {1,2,3,4,5,6,7,8,9}
F = {{},{1},{2},{3},{4},{5},{6},{7},{8},{9},S} as pairs of events cannot occur.
P(1) = ?, P(2) = ?, …
How can we assign the probabilities? Empirical frequency evidence is displayed for the use of Benford’s Law in many sources and even theoretical limiting justification was also derived to do the job.
The interesting psychological question is, how is it that it works so well at catching fraud? If people are faking data and consequently appeal to a false yet seemingly true sense of randomness, what other misconceptions are commonly held?
On the philosophical side, the subjective credence held by fakers of data is hugely disparate with empirical notions of this probability function P. Is there some fundamental axiom violation held by people or are they abiding by misused coherent axioms? That is, can some formal structure be defined so that non-omniscient beings can act “rationally”, Brian Weatherson in 2003 seems to tackle this problem.
Interpreting the word "Probability"
When the word "probability" was used above, it was in reference to the output of the mathematical function P. This function does not have closed-form in general and greatly changes depending on the stochastic scenario at hand and on what events are in F. In our coin flip example, the output of P was deduced by recognizing that the event H had 1 way to happen and was among 2 possibilities, thus 1/2 = 50% is the chance as it is also understood that each of the 2 events was equally likely. Irrespective of the agent observing this, the chance remains 50% and so this chance exists fundamentally outside of subjective perception. Other uses of the word may not include this quantification and only reference some subjective degree of belief (which does depend on the agent believing it). Some great minds have explored this so here I explore some of that thought.
Classical Interpretation
“the most important questions of life, are indeed for the most part only problems of probability”
To make this post of reasonable length, I will pick up here by expanding upon [5] in a future post.
References
Foundations of the Theory of Probability (1933) - Andrey Kolmogorov
Adam Caulton's blog (philosophy professor)
Philosophy of Probability: Contemporary Readings (2011) - Anthony Eagle
A Philosophical Essay on Probabilities - Pierre Simon Laplace
Aiden Lyon’s Intro to the Philosophy of Probability.