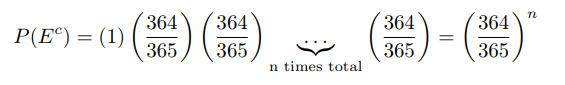Have you ever been sung to at a restaurant on your birthday? Usually this is for kids but it would be interesting to see how old a person has to be before it gets creepy to insist that the staff sing to you, leave a comment if you conduct this field research.
Here's the problem:
“If you worked at a restaurant and had to sing to someone for their birthday, what’s the required number of people in the party for there to be a 50% chance there are two birthday people? If this happens, you get a BOGO on having to sing! ”
A pug capturing the emotion of getting sung at by off-camera staff at the strangely named purple restaurant "Getty Images" for her birthday (colorized, 2018). Photo by LightFieldStudios/iStock / Getty Images
The problem is relevant to you since you care about singing as least as possible; something everyone (except Shakira and drunk people doing karaoke of Shakira) should strive to do. Mathematically speaking the problem has a simple counting solution but leads to a counter-intuitive solution so you might see it (or a variation of) talked about often on Reddit and this variation was even covered by Khan.
Consider the birthday boy/girl to be sung at, suppose their birthday falls on some date D. Imagine asking the other guests one at a time what their birthday is. The first guest has a 364/365 chance of not hitting the hosts’ birthday when asked as there are 364 other days that it could be. The second guest chimes in but also has a 364/365 chance of not hitting the right date D as we don’t care if guest 2 matches with guest 1, only that he/she match with the birthday boy/girl. Similarly each consecutive guest will have this same 364/365 chance of hitting that particular birthday. As each birthday is an independent event (if they weren't their parents would have some explaining to do) we can multiply their odds to get an inclusive probability of no-one else having the birthday D. Suppose there are "n" (other than the bday boy/girl) guests in the party, then the converse of the event E that there is no guest with the birthday of D is:
The superscript c denotes the event "not E", i.e no one else having D as their birthday.
We can use the encompassing property of probability to get the event probability itself:
The only two options are E or not E. As a result, subtract the probability of not E from 100 percent to get the probability of E
The question, for you the waiter doing this in your head, is what should "n" be in the above probability so that it is greater than fifty percent? You cower back to the kitchen entrance and scribble the following out on a napkin (algebra students, please check my work):
“We conclude that there has to be greater than 253 people in the party for the waiter to have a 50% chance at getting two birthdays with one song. Hopefully they leave a tip! ”
Note that this variation is different than the traditional one in the sense that we fixed the birthday D ahead of time! The traditional problem dictates only that two people share any birthday which obviously opens up more possibilities. To illustrate this, I have graphed the traditional problem in blue against our problem in red. The MATLAB code to generate this is here.
Fixed the birthday ahead of time as in our problem (red) against just simply having two shared birthdays among the party (that could be any date, blue). Think about how to use the same reasoning we used in the red case to see how I generated the blue case.