Karl Weierstrass and the Function S'more
History
The cheery mug of Karl Weierstrass [1], known as the father of analysis.
In 1885 Karl Weierstrass wrote down his most famous theorem often referred to as the "Stone-Weierstrass Theorem" in analysis textbooks. The theorem itself is the quintessential constructive theorem and as it turns out, can be proved using very different approaches; this makes the theorem elegant as well as perfect for broadening ones purview of maths.
One is hard pressed to not run into the name Weierstrass in the analysis field, and for good reason. There are a multitude of results and methods a second-semester calculus student might read penned by him. Interestingly, the man had apprehensions about studying mathematics and only after "four years of intensive fencing and drinking" [1] did Weierstrass formally pursue mathematics. Refreshingly enough there seems to exist some kind of modern type of soul-searching and purpose-seeking in the story of Weierstrass.
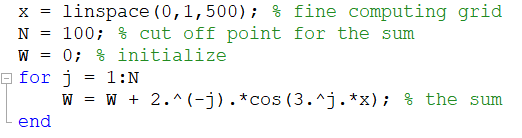
In 1872 to the dismay of analysts, Weierstrass discovered (constructed) a function which is continuous everywhere but differentiable nowhere. This surprising and counterintuitive construction completed an effort by Riemann himself and is graphed below.
Figure 1: For every x, the above function is continuous but not differentiable!
The Problem and Quick Solution
The interesting question posed from here, is can one find a polynomial (a nice function) to approximate such a horrendous function as Figure 1? A classic problem first seen in second semester calculus, we want to defer, out of sheer hardness of the current function, to a set of "nicer" functions. I define "nicer" for my students here to mean differentiation and integration both become trivial when considering simple polynomials. This is quite the problem! How is one to pull an approximant (or sequence of approximants) out of thin air?
Solution: Yes, here it is:
Figure 2: The solution (red) to approximating Weierstrass' nasty function (blue)
Imagine lighting a big fire underneath Figure 1 in order to "melt" the cheesy function a bit. This is what I have graphed in red in Figure 2 and clearly it does the job at hand. It is a smoother/nicer function to work with while still reminding us of its original.
The Problem and Detailed Proof
Here I will state and prove Weierstrass' Theorem by constructing a heat equation with specific initial conditions and then solving my own proposition. Since all cool authors number the theorems, I have to maintain face.
Without loss of generality we can extend f to a function on the whole real line and we can consider the bounded domain as the standard [-1,1] by frivolous scaling. Consider the heat equation:
The solution to which is well known as a heat kernel convolution:
As u is entire for positive time it is real-analytic, whence it can be represented by a Taylor series. This Taylor series can be truncated to get an arbitrarily ordered polynomial approximation to f by taking the limit as t goes to 0 (time shrinks back to not melting the function). This convergence is uniform on compact subsets of real numbers and so is pointwise everywhere.
References
- This biography of Weierstrass
- Approximation Theory and Approximation Practice - Nick Trefethen
- K R Biermann, Biography in Dictionary of Scientific Biography (New York 1970-1990).